小结
我们已经推导出了卡尔曼滤波全部的五个方程的矩阵形式,我们现在把它们汇总在一起。
卡尔曼滤波执行的是一个“预测-修正”循环,如下图所示。

一旦初始化完成,卡尔曼滤波首先预测下一时刻的系统状态,并且同时给出这个预测的不确定性。
随后拿到测量结果,卡尔曼滤波会更新(或修正)这个预测值及其不确定性,并且同时再进行下一时刻的预测,以此类推。
下图给出了卡尔曼滤波运算的全貌。
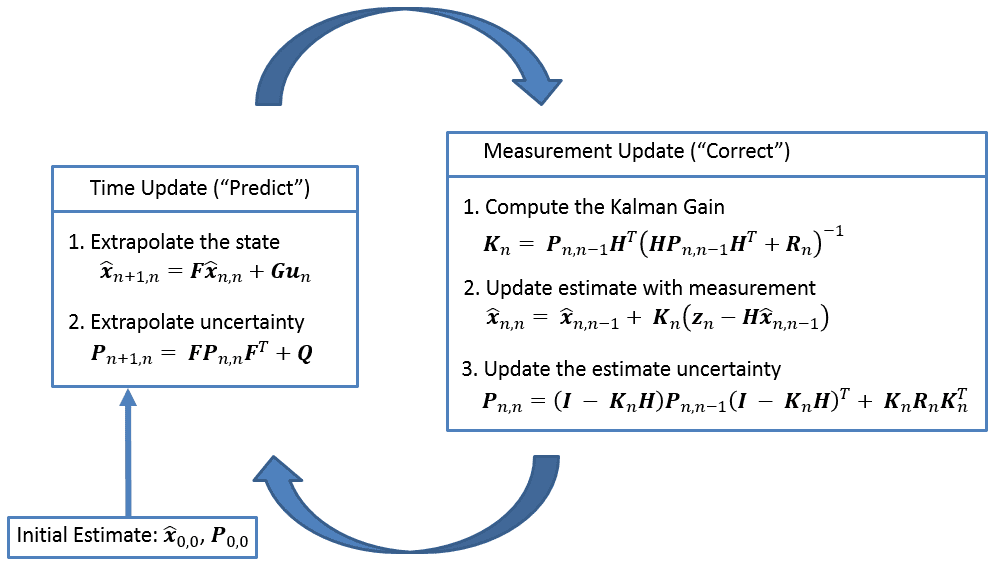
下表给出了卡尔曼滤波全部的方程。
| 方程 | 方程名 | 别名 | |
|---|---|---|---|
| 预测 | \( \boldsymbol{\hat{x}}_{n+1,n} = \boldsymbol{F\hat{x}}_{n,n} + \boldsymbol{Gu}_{n} \) | 状态外插 |
预测器方程 转移方程 预测方程 动态模型 状态空间模型 |
| \( \boldsymbol{P}_{n+1,n} = \boldsymbol{FP}_{n,n}\boldsymbol{F}^{T} + \boldsymbol{Q} \) | 协方差外插 | 预测器协方差方程 | |
| 更新 (修正) |
\( \boldsymbol{\hat{x}}_{n,n} = \boldsymbol{\hat{x}}_{n,n-1} + \boldsymbol{K}_{n} (\boldsymbol{z}_{n} - \boldsymbol{H\hat{x}}_{n,n-1} ) \) | 状态更新 | 滤波方程 |
| \( \boldsymbol{P}_{n,n} = \left(\boldsymbol{I} - \boldsymbol{K}_{n}\boldsymbol{H} \right) \boldsymbol{P}_{n,n-1} \left(\boldsymbol{I} - \boldsymbol{K}_{n}\boldsymbol{H} \right)^{T} + \boldsymbol{K}_{n}\boldsymbol{R}_{n}\boldsymbol{K}_{n}^{T} \) | 协方差更新 | 修正方程 | |
| \( \boldsymbol{K}_{n} = \boldsymbol{P}_{n,n-1}\boldsymbol{H}^{T}\left(\boldsymbol{HP}_{n,n-1}\boldsymbol{H}^{T} + \boldsymbol{R}_{n} \right)^{-1} \) | 卡尔曼增益 | 权重方程 | |
| 辅助方程 | \( \boldsymbol{z}_{n} = \boldsymbol{Hx}_{n} \) | 测量方程 | |
| \( \boldsymbol{R}_{n} = E\left( \boldsymbol{v}_{n}\boldsymbol{v}_{n}^{T} \right) \) | 测量协方差 | 测量误差 | |
| \( \boldsymbol{Q}_{n} = E\left( \boldsymbol{w}_{n}\boldsymbol{w}_{n}^{T} \right) \) | 过程噪声协方差 | 过程噪声误差 | |
| \( \boldsymbol{P}_{n,n} = E\left( \boldsymbol{e}_{n}\boldsymbol{e}_{n}^{T} \right) = E\left( \left( \boldsymbol{x}_{n} - \boldsymbol{\hat{x}}_{n,n} \right) \left( \boldsymbol{x}_{n} - \boldsymbol{\hat{x}}_{n,n} \right)^{T} \right) \) | 估计协方差 | 估计误差 |
下表汇总了符号(包括其他文献中的不同记法)和对应维度。
| 项 | 名称 | 其他记法 | 维度 |
|---|---|---|---|
| \( \boldsymbol{x} \) | 状态向量 | \( n_{x} \times 1 \) | |
| \( \boldsymbol{z} \) | 输出向量 | \( \boldsymbol{y} \) | \( n_{z} \times 1 \) |
| \( \boldsymbol{F} \) | 状态转移矩阵 | \( \boldsymbol{\Phi,A} \) | \( n_{x} \times n_{x} \) |
| \( \boldsymbol{u} \) | 输入向量 | \( n_{u} \times 1 \) | |
| \( \boldsymbol{G} \) | 控制矩阵 | \( \boldsymbol{B} \) | \( n_{x} \times n_{u} \) |
| \( \boldsymbol{P} \) | 估计协方差 | \( \boldsymbol{\Sigma} \) | \( n_{x} \times n_{x} \) |
| \( \boldsymbol{Q} \) | 过程噪声协方差 | \( n_{x} \times n_{x} \) | |
| \( \boldsymbol{R} \) | 测量协方差 | \( n_{z} \times n_{z} \) | |
| \( \boldsymbol{w} \) | 过程噪声向量 | \( \boldsymbol{y} \) | \( n_{x} \times 1 \) |
| \( \boldsymbol{v} \) | 测量噪声向量 | \( n_{z} \times 1 \) | |
| \( \boldsymbol{H} \) | 观测矩阵 | \( \boldsymbol{C} \) | \( n_{z} \times n_{x} \) |
| \( \boldsymbol{K} \) | 卡尔曼增益 | \( n_{x} \times n_{z} \) | |
| \( \boldsymbol{n} \) | 离散时间变量 | \( \boldsymbol{k} \) |
维度注解:
- \( n_{x} \) 是状态向量中的状态个数
- \( n_{z} \) 是测量到的状态个数
- \( n_{u} \) 是输入向量中的元素个数
